|
Was bedeutet „Höhe“?
Brockhaus Bilder-Conversations-Lexikon für das deutsche Volk, 1841:
„Die Höhe eines Punktes über einer Ebene heißt die Länge der senkrechten Linie, welche vom Punkte auf die Ebene herabgelassen wird, oder, was Dasselbe, die Entfernung des Punktes von der Ebene. Bei einem Körper nennt man die Höhe die größte Entfernung, um welche irgendein Punkt an der Oberfläche des Körpers von derjenigen Ebene absteht, welche als die Grundfläche des Körpers angenommen worden ist. Da auf der Erde, wenn man dieselbe als eine Kugel betrachtet, das Wasser aller großen Meere sich so vertheilen muß, daß es überall gleichweit von dem Mittelpunkte der Erde absteht, so pflegt man die Höhen der Punkte auf der Erdoberfläche, z. B. der Spitzen der Berge, nach der Erhebung derselben über die Meeresoberfläche (das Niveau oder den Spiegel des Meeres) zu bestimmen. Indeß wird häufig auch die Höhe eines Gegenstandes über einer andern Ebene, z. B. eines Thurmes über der Fläche, auf welcher er steht, gesucht.“
Aus dem Online-Lexikon Wikipedia:
Die Höhe ist der lotrechte Abstand von einer Referenzfläche. Dies kann zum einen die Erdoberfläche, ein mittlerer Meeresspiegel, oder eine Fläche durch einen Punkt des Objekts selbst sein. Die Höhe ist eine eindimensionale Größe und wird meist in Längeneinheiten gemessen. Die Höhe von Bauwerken ist die lotrechte Ausdehnung vom Boden bis zum höchsten Punkt. Teile unter der Erde (wie Keller und das Fundament) zählen im allgemeinen nicht zur Höhe. Die Höhe eines Hochsprunges wird ebenfalls über dem Boden (Absprunghöhe) gemessen. Bei der Flughöhe ist eine Messung über Grund oder über Meeresspiegel üblich.
In der Geodäsie benutzt man als Höhenreferenzfläche das Geoid oder auch ein Referenzellipsoid. Die Höhe dieser Bezugsflächen wird an einem Pegel festgemacht. Hier finden vor allem Normalnull, aber auch Meter über Adria oder Seekartennull Anwendung und bilden dabei die Grundlage eines jeden Höhensystems.
Höhendefinition
Die eigentliche Meßgröße bei der Höhenbestimmung ist nicht die Meereshöhe, sondern eine Höhendifferenz. Diese werden wie folgt definiert:
1. geometrisch - als Differenz zweier Höhen, ausgedrückt in einem Längenmaß.
2. physikalisch als Differenz zweier Schwerepotentiale.
Höhen können nicht gleichzeitig geometrisch und physikalisch korrekt sein.
Zwischen den beiden darauf basierenden Höhensystemen bestehen merkliche Unterschiede, die im Hochgebirge Größenordnungen von cm...dm pro Kilometer erreichen können. Die Ursache hiefür sind Unregelmäßigkeiten im Erdschwerefeld, weil die Erde weder eine genaue Kugel, noch inwendig homogen aufgebaut ist. Diese Effekte werden seit etwa 100 Jahren unter den Begriffen Lotabweichung bzw. Schwereanomalie und Geoid erforscht und heute ausreichend genau meßtechnisch erfaßt.
Geometrisch definierte Höhen werden heute als Ellipsoidische Höhe bezeichnet. Diese geben den Abstand eines Punktes von einem Referenzellipsoiden entlang der Ellipsoidnormalen an. Zwei Punkte gleicher ellipsoidischer Höhe liegen jedoch nicht auf der selben Äquipotentialfläche, so daß zwischen ihnen Wasser fließen kann.
-
Ellipsoidische Höhen können seit einiger Zeit direkt mittels Satelliten bestimmt werden - was früher die Anlage eines Raumpolygonzuges erforderte. Bei GPS beispielsweise werden die Positionen von zwei oder mehr Antennen gleichzeitig ausgewertet. Kennt man nun die Höhe eines Punktes (z. B. eines Vermessungspunktes), kann man aus den ermittelten Höhenunterschieden die anderen Punkthöhen berechnen.
- Terrestrisch können ellipsoidische Höhendifferenzen nur nach entsprechender Reduktion wegen Lotabweichung bzw. Geoidundulation bestimmt werden. Die reine Messung erfolgt z. B. mit einem Theodolit, die Lotabweichung (in den Alpen bis 40" oder 0,01°) wird an die gemessenen Vertikalwinkel als kleine Korrektur angebracht. Tut man das nicht (wie früher mangels genauer Daten), so erhält man eine Mischform der Höhen.
Physikalisch definierte Höhen werden auch Dynamische Höhen genannt und hängen direkt mit dem Schwerefeld bzw. dem Wasserspiegel zusammen. Sind sie noch nicht mit der Schwerebeschleunigung g in die Dimension Meter umgerechnet, nennt man sie Geopotentielle Koten.
Dynamische Höhen können nur auf der Erdoberfläche gemessen werden, und keineswegs mit Satelliten.
-
Die gebräuchlichste Methode ist das Nivellement, bei dem mit einem horizontalen Visur die Höhendifferenz auf zwei Messlatten abgelesen wird. Weil die Horizontale unmittelbar dem Schwerefeld entspricht, kann zwischen zwei Punkten gleicher Höhe kein Wasser fließen. Bei größeren zurückgelegten Strecken muß jedoch das Nivellement mittels Gravimetrie ergänzt und reduziert werden, da Äquipotentialflächen keine konstanten geometrischen Abstände aufweisen. Bei einer 100 km langen Schleife - etwa entlang der Täler und Pässe rund um den Großglockner - kann der Widerspruch einige Zentimeter betragen.
- Weitere Methoden für dynamische Höhenmessung sind die Schlauchwaage (bis zu 0,01 mm genau) und das Staffeln.
Mischformen
Die besonders ökonomische ("trigonometrische") Höhenmessung mit dem Theodolit liefert eine "Mischhöhe", die eine Art Kompromiß zwischen den einander ausschließenden geometrischen und physikalischen Systemen darstellen.
Die wichtigste, für die Praxis meist bevorzugte Mischhöhe ist die Orthometrische Höhe. Man erhält sie durch die "orthometrische Reduktion" des Nivellements oder durch die Lotabweichungsreduktion der trigonometrischen Meßmethoden.
Im Gegensatz zu der auf das Referenzellipsoid des Geoids bezogene „relative Höhe“ kann speziell bei Bergen auch eine quasi „absolute Höhe“ diskutiert werden, die sich auf den Erdmittelpunkt bezieht. Danach wäre nicht mehr der Mt. Everest, sondern der Chimborazo der höchste Berg der Erde.
| |
Geographische Breite
|
1
Höhe über dem Meeresspiegel in Meter
|
2
Basisradius dort in Meter
|
3
N in Meter
|
1 + 2 + 3 = 4
Tatsächlicher Abstand vom Erdmittelpunkt in Meter
|
| Chimborazo |
1°28´S |
6310 |
6378123 |
20 |
6384410 |
| Huascarán |
9° 12´S |
6768 |
6377600 |
20 |
6384388 |
| Cotopaxi |
0° 40´S |
5897 |
6378134 |
20 |
6384051 |
| Kilimandscharo |
3° 04´S |
5895 |
6378076 |
— 20 |
6383951 |
| Everest |
27° 59´N |
8848 |
6373430 |
— 27 |
6382251 |
Der Chimborazo ist mit 6384453 Meter Abstand vom Erdmittelpunkt 2202 Meter „höher“ als der Mount Everest!
(Mit fast der gleichen Berechtigung könnte man auch sagen: Der Chimborazo ist der Sonne am nächsten; dies gilt aber nur über das Jahr gemittelt.)
Die allgemeine Berechnungsformel für den Erd-Ellipsoid geht so: R = Re[1 - f.sin2(geographische Breite)]
Dabei ist Re der Radius am Äquator und f die Abplattungsrate. Die genauesten Zahlen für den ganzen Erdball sind mit dem WGS84 (World Geodetic System 1984) vorgegeben: Re = 6378137 m, f = 1/298,257 = 0,00335281. Die Erdgestalt weicht durch lokale Variationen in der Dichte der Erdkruste auch vom idealen Ellipsoiden ab: Über Stellen mit hoher Dichte erweitert sich die Meereshöhe zu einer „Beule“. Da sich die Berghöhen auf die lokalen Meereshöhen beziehen, muß ein lokaler Streufaktor N zum Basisradius des Ellipsoiden addiert oder von ihm subtrahiert werden.

Mancher Berg trägt Vermessungspunkt und „Pyramide“.
Relatives und Absolutes
Was dabei als „hoch“ angesehen wird, ist stets relativ zur umgebenden Landschaft. So würden die Dammer Berge in Niedersachsen (115 bis 146 m) in der Schweiz nur als Hügel gelten, wofür man in üblicherweise die Grenze bei etwa 300 m ansetzt. Der Himmelbjerget (Himmelsberg) gilt manchen als höchster Berg Dänemarks, mißt jedoch weniger als die tatsächlich höchsten Punkte Dänemarks, und der Wilseder Berg überragt mit 169 m über NN nicht nur die Lüneburger Heide, sondern den Umkreis von 100 Kilometer.
Die Schartenhöhe und die Dominanz einer Erhebung können als Kriterien herangezogen werden, um einen Gipfel als selbständigen Berg zu klassifizieren. Im Hochgebirge gilt z.B. eine Schartenhöhe von ca. 100 m bis 300 m und eine Dominanz von ca. 1 km bis 3 km als Mindestmaß, um von einem eigenständigen Berg zu sprechen.
Unter der Schartenhöhe versteht man die Höhendifferenz zwischen einem Berggipfel und der höchstgelegenen Scharte, über die man einen höheren Gipfel erreichen kann; die Dominanz bezeichnet den Abstand des Gipfels zum nächsten Punkt gleicher Höhe.
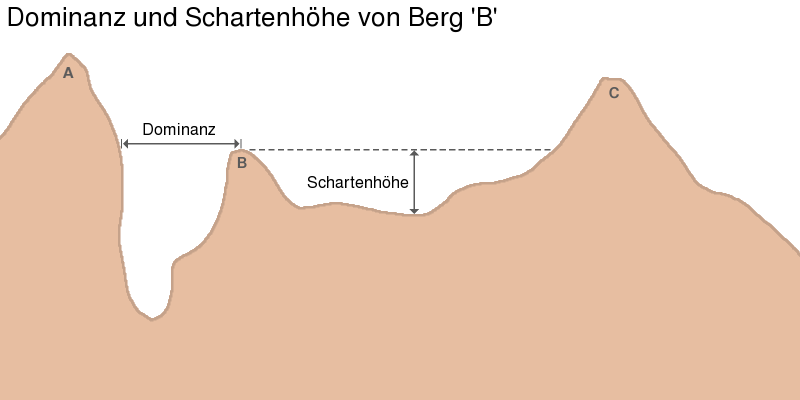
Die Schartenhöhe (auch als Prominenz oder Schartentiefe bezeichnet) ist daher ein Maß für die Selbständigkeit eines Berges und neben der Dominanz ein wichtiges Kriterium einen Gipfel als Berg zu klassifzieren. Je höher die Schartenhöhe ist, desto freistehender wirkt ein Berg. Die Schartenhöhe gibt somit an, wie viele Höhenmeter man mindestens absteigen muß, um auf den nächsthöheren Berg zu gelangen. Bei einer Erhebung auf einem Grat ist die Schartenhöhe meist sehr gering und man spricht dann von einem Nebengipfel oder einer Graterhebung, und nicht von einem freistehendem Berg. Je nach Definition und Gegend gilt eine Schartenhöhe von ca. 300 Metern als Mindestmaß, um von einem eigenständigen Berg zu sprechen.
| Berg |
m |
ft |
P |
OD |
Land |
| Ätna |
3323 |
10902 |
3323 |
100,00 |
Italien |
| Mont Blanc |
4807 |
15771 |
4700 |
97,77 |
Frankreich |
| Aneto |
3404 |
11168 |
2812 |
82,61 |
Spanien |
| Großglockner |
3798 |
12461 |
2423 |
63,80 |
Österreich |
| Marmolada |
3342 |
10965 |
2132 |
63,79 |
Italien |
| Wildspitze |
3772 |
12375 |
2264 |
60,02 |
Österreich |
| Piz Bernina |
4049 |
13284 |
2234 |
55,17 |
Schweiz |
|
Haute Cime
|
3257 |
10686 |
1796 |
55,14 |
Frankreich |
| Monte Viso |
3841 |
12602 |
2075 |
54,02 |
Italien |
| Antelao |
3263 |
10705 |
1746 |
53,51 |
Italien |
| Finsteraarhorn |
4274 |
14022 |
2269 |
53,09 |
Schweiz |
| Ortler |
3905 |
12812 |
1953 |
50,01 |
Italien |
| Barre des Écrins |
4101 |
13455 |
2043 |
49,82 |
Frankreich |
| Presanella |
3556 |
11667 |
1672 |
47,02 |
Italien |
| Dufourspitze |
4634 |
15203 |
2165 |
46,72 |
Schweiz |
Die prominentesten Berge Europas, mit der Meereshöhe der „Prominenz“ P und der „Orographischen Dominanz“ OD gegenübergestellt. OD = Prominenz/Meereshöhe x 100, ein Maß der Selbständigkeit der Erhebung.
Literatur:
„Die bloße Aussage, daß ein Berg eine vertikale Höhe von soundsoviel Metern über dem Meeresspiegel besitzt und soundsoviele Tonnen Granit enthält, bedeutet überhaupt nichts. Der Montblanc ist ungefähr drei Meilen hoch. Na und? Drei Meilen entsprechen einem einstündigen Spaziergang für eine Lady, einer Taxigebühr von acht Pence, das heißt der Strecke von Hyde Park Corner bis zur South Bank – ein Schnellzug könnte sie in drei und ein Rennpferd in fünf Minuten zurücklegen.“
Lesley Stephen – 1832 – 1904 – „Playground of Europe”, 1871
Merke: Nichts kann so einfach sein, als daß es nicht kompliziert gemacht werden könnte!
|

